문제 설명(요약)
3차원 공간에 \(N\)개의 점 \(P_1(x_1,y_1,z_1)\), \(\cdots\), \(P_N(x_N,y_N,z_N)\)이 주어져 있다. (정수좌표)
다음 조건을 만족하는 두 정육면체 \(Q\), \(Q'\)을 생각하자.
- \(Q\)와 \(Q'\)의 중심은 서로 일치한다.
- 주어진 \(N\)개의 점은 \(Q\)의 내부 또는 경계에 있으며, 동시에 \(Q'\)의 외부 또는 경계에 있다. 즉, \(Q\)는 바깥쪽 정육면체이고 \(Q'\)은 안쪽 정육면체이다.
\(Q\)와 \(Q'\)의 한 변 길이의 차이의 최솟값을 구하시오.
제약 조건: \(N \le 15,000\), \(-10^9 \le x_i, y_i, z_i \le 10^9\)
실행 조건: 테스트 케이스 50개에 대한 실행시간 총합 10초 이내, 메모리 총합 256MB 이내
풀이
문제를 풀기 위해서는 3차원 탐색을 2차원으로 국한시키는 것이 첫 번째 발상이다.
왜 그런지 살펴보기 위해, 주어진 점들의 Bounding box \(B\)를 생각하자. 그리고 \(B\)의 가장 긴 변의 길이를 \(L\)라고 하자.
보조정리 1. \(Q\)의 한 변 길이가 \(L\)인 최적해가 반드시 존재한다.
(증명) 우선, \(Q\)는 주어진 모든 점을 포함해야 하므로 \(B\)를 포함할 수밖에 없다. 그러므로 \(Q\)의 한 변 길이는 반드시 \(L\)보다 크거나 같다.
그러므로 \(Q\)의 한 변 길이가 \(L\)보다 클 경우를 생각하자. 이 경우 목적함수의 값을 증가시키지 않으면서 \(Q\)의 한 변 길이가 \(L\)가 되도록 반드시 변형할 수 있다.
왜냐고? \(Q\) 내부에 한 변 길이가 \(L\)이면서 \(B\)를 완전히 포함하는 정육면체 \(R\)를 잡자. 정육면체 \(S\)의 중심을 \(C(S)\)로 나타낸다고 하자. 이제 중심을 \(C(R)\)로 옮기는 상황을 생각하자. \(Q\)의 한 변 길이를 \(L + 2\alpha\)라고 하면(단, \(\alpha > 0\)), 바깥쪽 정육면체의 한 변 길이는 \(Q\)와 비교하여 \(2\alpha\)만큼 줄어들었다.
이제 안쪽 정육면체의 한 변 길이의 변화 범위를 생각해보자. 우선, \(C(R)\)과 \(C(Q)\)사이의 택시거리는 \(\alpha\)에 의해 그 크기가 제한된다. 구체적으로는, \(C(R) - C(Q) = (dx,dy,dz)\)라고 하면,
$$ |dx|, |dy|, |dz| \le \alpha. $$
중심을 \(C(R)\)로 옮겼을 때의 안쪽 정육면체를 \(R'\)이라고 하면, \(R'\)의 한 변 길이는 \(Q'\)에 비해 \(2\alpha\)를 초과하여 감소하지 않는다. 그 이유는 기존 중심 \(C(Q)\)에서 \(Q'\)의 면까지의 거리가 \(L'/2\)였다고 하면, 새로운 중심 \(C(R)\)에서 \(Q'\)의 면까지의 거리는 각각 \(L'/2 - |dx|\), \(L'/2 - |dy|\), \(L'/2 - |dz|\)이므로, 최소한 한 변의 길이가 $$ 2\times\min\lbrace L'/2 - |dx|, L'/2 - |dy|, L'/2 - |dz| \rbrace \ge L' - 2\alpha $$인 내부 정육면체를 만들 수 있음이 보장되기 때문이다. 한편, 그보다 더 큰 내부 정육면체를 만들 수 있게 된다고 하더라도 이는 솔루션을 더 좋아지게 할 뿐, 나빠지게 하지는 않으므로 문제가 없다.
따라서 임의의 정육면체 순서쌍 \(Q, Q'\)에 대하여, 바깥쪽 정육면체 한 변 길이가 \(L\)이면서 목적함수 값은 원래보다 작거나 같은 정육면체 순서쌍 \(R, R'\)을 항상 찾을 수 있다. ■
보조정리 1에 의해 우리는 \(Q\)의 한 변 길이가 \(L\)인 정육면체 \(Q\)만 후보군으로 고려하면 된다. 그런데 이러한 상황에서는 \(C(Q)\)가 2차원 직사각형 위에서만 움직인다. 왜냐면, Bounding box \(B\)의 세 축 중 적어도 한 축 이상에 대하여 반드시 "꽉 붙어 있어야" 하기 때문이다. 따라서 \(C(Q)\)는 \(B\)의 한 변 길이가 \(L\)인 축을 수직이등분하는 평면 내부로 제한된다. 이 평면 위에서 \(B\)가 \(Q\)에 포함되어야 함을 생각하면 \(C(Q)\)의 범위가 직사각형으로 제한된다는 것을 알 수 있다. (Note: 만약 \(B\)의 두 변의 길이가 모두 \(L\)이라면 중심점의 후보는 선분이 되고, \(B\)가 정육면체라면 중심점의 후보는 한 점으로 결정된다.)
\(Q\)의 한 변 길이가 \(L\)로 고정됨에 따라 \(Q'\)의 한 변 길이의 최댓값을 찾는 문제로 환원되었다.
이후의 논의에서 \(C(Q)\)가 움직일 수 있는 2차원 직사각형을 \(K\)라고 부르자.
예제 2. 만약 평면이 \(z = 0\)이고 어떤 점의 좌표가 \((0, 0, 1)\)이라면, 다음과 같은 형태의 제한조건이 주어질 것이다.
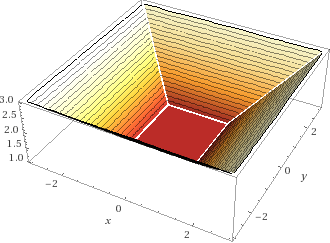
원리적으로는 이러한 형태의 함수 \(N\)개의 최솟값 함수를 영역 \(K\)에서 최대화하면 된다. 하지만 그것을 \(o(N^2)\) 시간에 하기에는 복잡하게 느껴진다.
만약 결정 문제로 바꾸어 생각하면 어떨까? \(Q'\)의 한 변 길이가 \(h\)일 수 있다면, 그보다 작은 한 변 길이는 어떤 값이든지 가능할 것이다. 따라서 이진 탐색이 가능하다. 이때 점 \(P_i\)가 주는 제한조건은
- Case 1. \(K\)를 포함하는 평면으로부터의 거리가 \(h/2\) 이상일 경우: 제한으로 작용하지 않음.
- Case 2. \(K\)를 포함하는 평면으로부터의 거리가 \(h/2\) 미만일 경우: \(P_i\)를 \(K\) 위로 정사영한 점 \(P_i^\prime\)을 중심으로 하고, 한 변의 길이가 \(h\)인 정사각형은 "금지 영역"이 된다. 단, 경계는 금지 영역에 포함되지 않음.
즉, 이 정사각형들이 \(K\)를 전부 덮는다면 \(h\)가 불가능하고, 전부 덮지 못한다면 \(h\)가 가능하다. 이는 고전적인 Plane Sweeping 문제로, Segment Tree with Lazy Propagation을 이용해 풀 수 있다. (BOJ 7626과 완전히 동일)
이제 이진 탐색을 도입하면 쉽게 풀 수 있다. 이를 정당화하기 위해, 보조정리를 하나 증명하자.
보조정리 3. 최적해의 값은 반드시 0.5의 정수배이다.
(증명) \(K\) 내부에서 어떤 점 \(P_i\)에 의한 제한조건은 다음 그림처럼 나타난다. 예제 2의 함수를 평면상에 투영한 꼴이기 때문이다.

이때 빨간 정사각형의 각 꼭짓점은 반드시 정수좌표에 있다. (입력점이 정수좌표로 주어지기 때문)
"정수좌표에서 그은 좌표축에 평행한 직선 혹은 기울기가 -1, +1인 직선" 사이의 교점이 있다면 반드시 0.5의 정수배 격자점이다.
위 그림이 여러 개 중첩된 모양도 결국 "정수좌표에서 그은 좌표축에 평행한 직선 혹은 기울기가 -1, +1인 직선"들로만 이루어져 있으므로, 모든 교점은 반드시 0.5의 정수배 격자점이다.
"정수좌표에서 그은 좌표축에 평행한 직선 혹은 기울기가 -1, +1인 직선"으로 분할된 영역은 반드시 직각이등변삼각형으로 더 분할할 수 있다. 그런데 원래의 함수(예제 2)를 보면 piecewise linear 함수이므로, 각 직각이등변삼각형 내에서 목적함수의 값은 linear이다. 직각이등변삼각형은 볼록영역이고 linear 함수는 볼록함수이므로 최댓값은 반드시 직각이등변삼각형의 세 꼭짓점 중 하나에서 발생한다. 그런데 모든 교점은 반드시 0.5의 정수배 격자점이므로, \(K\)에서 목적함수의 최댓값은 반드시 0.5의 정수배이다. ■
따라서 입력좌표에 모두 2를 곱해주면 목적함수의 최댓값은 반드시 정수가 되므로 이진탐색이 수월해진다.
이진탐색을 수행하여 구한 \(h\)값을 \(H\)라고 하면, 구하는 최적해의 값은 \(L-H\)가 된다.
이진탐색을 \(O(\lg 10^9)\)번 수행하고, 각 이진탐색은 \(O(N \lg N)\)의 시간이 소요되므로, 전체 수행시간은 \(O(N \lg N \cdot \lg 10^9)\)이다. \(N \le 15,000\)이므로 10초 내에 충분히 통과할 수 있다.
구현 노트
1. 이진 탐색에서 가능 여부를 판정할 때, 정사각형의 경계 처리에 유의해야 한다. \(K\)는 경계를 포함하여 생각해야 하며, 제한조건이 되는 정사각형의 경우 경계를 제외하고 생각해야 한다. 이를 쉽게 할 수 있는 방법은 격자를 면적으로 생각하는 것이다. 즉, \(K\)의 좌표가 \((a,b) - (c,d)\)로 주어진다면 경계를 포함하기 위해 \((a,b) - (c+1,d+1)\)로 생각할 수 있으며, 금지 정사각형의 좌표가 \((a,b) - (c,d)\)로 주어진다면 경계를 제외하기 위해 \((a+1,b+1) - (c,d)\)로 생각할 수 있다. 이렇게 면적 중심으로 변환한 후에는 경계를 신경 쓸 필요 없이 Plane Sweeping을 진행하면 된다.
2. (면적 중심으로 변환한 후) 금지 정사각형이 \(K\)를 벗어나는 부분이 있다면 Plane Sweeping 이전에 Clipping을 해준다. 겹치는 면적이 1 이상 있을 경우에만 Clipping하여 Sweeping시 포함하고, 그렇지 않다면 아예 Drop해도 된다. 어차피 \(K\) 내부에 제한조건으로 작용하지 않기 때문이다.
3. 1과 2대로 했다면, Plane Sweeping을 진행하여 나온 총 면적이 (면적 중심으로 변환한 후의) \(K\)의 면적과 일치하는지를 확인하는 것으로 판정할 수 있다. 일치하면 다 덮은 것이므로 불가능, \(K\)의 면적보다 작으면 다 덮지 못한 것이므로 가능이다. (Plane Sweeping 코드를 변형 없이 사용할 수 있다는 뜻)
4. Plane Sweeping 시에는 좌표압축을 적용하여야 서로 다른 y좌표의 개수가 \(O(N)\)개로 줄어 Segment Tree로 대응이 가능하다. 이때 이진탐색 단계마다 금지 정사각형의 크기가 달라지므로, 좌표압축 변환 테이블을 매번 새로 구축해야 한다.
Acknowledgement
cgiosy님의 SCPC 2019 1차예선 5번 풀이를 기반으로 일반화하여 풀이할 수 있었습니다. 좋은 풀이를 작성해주셔서 감사합니다.
이걸 이해하고 본선에 갔어야 하는데 말입니다...
'알고리즘 문제풀이' 카테고리의 다른 글
| SCPC 2020 1차예선 4번 구현 소스 코드 (0) | 2020.08.22 |
|---|---|
| SCPC 2020 1차예선 풀이, 후기 (11) | 2020.08.22 |
| SCPC 2019 본선 후기 (0) | 2019.07.30 |
| SCPC 2019 2차예선 4번 구현 소스 코드 (0) | 2019.07.06 |
| SCPC 2019 2차예선 풀이, 후기 (15) | 2019.07.06 |

