POI 18회 스테이지3 문제2. Monotonicity 2
문제 설명 https://www.acmicpc.net/problem/8195 풀이 * 아래 풀이는 POI 공식 사이트에서 볼 수 있는 풀이(폴란드어로 쓰여 있음)를 참조했습니다. (https://oi.edu.pl/) 1. 개요 우리가 해결할 문제는, 주어진 수열 \(a_1, a_2, \dots, a_n\)의 부분수열 \(a_{b_1}, a_{b_2}, \dots, a_{b_k}\) 중, 모든 \(1 \le i \le n-1\)에 대해 \(i\)번째 항과 \(i+1\)번째 항 사이에 \(a_{b_i} \,\langle s_i \rangle\, a_{b_{i+1}}\)이 성립하는 것 중 가장 긴 것을 찾는 것이다. 여기서 \(\langle s_i \rangle \)는 부등호 또는 등호인 \(s_i\)를 \(..
더보기
 SCPC 2020 1차예선 풀이, 후기
올해 SCPC는 작년보다 푸는 시간이 더 빨라진 것 같다! 알고리즘에 따라 나누어 보면 1번 그리디, 2번 DP, 3번 DP, 4번 세그먼트 트리, 5번 기하가 출제되었다. 구현 소스 코드 링크: 1번, 2번, 3번, 4번(별도의 글), 5번(별도의 글) 문제 1. 다이어트 설명 길이 \(N\)인 두 수열 \(A[1..N]\), \(B[1..N]\)이 주어져 있을 때, 두 수열에서 숫자를 각각 하나씩 뽑아 순서쌍 \((A[i], B[j])\)를 만드는 작업을 \(K\)번 반복하였다. 만들어진 \(K\)개의 순서쌍에서 두 수의 합의 최댓값을 최소화하도록 순서쌍들을 뽑으면 그 값은 얼마인가? (단, 한 번 쓴 수는 다시 쓰지 않는다.) 제한조건: \(1 \le N \le 200,000\), \(1 \le K..
더보기
SCPC 2020 1차예선 풀이, 후기
올해 SCPC는 작년보다 푸는 시간이 더 빨라진 것 같다! 알고리즘에 따라 나누어 보면 1번 그리디, 2번 DP, 3번 DP, 4번 세그먼트 트리, 5번 기하가 출제되었다. 구현 소스 코드 링크: 1번, 2번, 3번, 4번(별도의 글), 5번(별도의 글) 문제 1. 다이어트 설명 길이 \(N\)인 두 수열 \(A[1..N]\), \(B[1..N]\)이 주어져 있을 때, 두 수열에서 숫자를 각각 하나씩 뽑아 순서쌍 \((A[i], B[j])\)를 만드는 작업을 \(K\)번 반복하였다. 만들어진 \(K\)개의 순서쌍에서 두 수의 합의 최댓값을 최소화하도록 순서쌍들을 뽑으면 그 값은 얼마인가? (단, 한 번 쓴 수는 다시 쓰지 않는다.) 제한조건: \(1 \le N \le 200,000\), \(1 \le K..
더보기
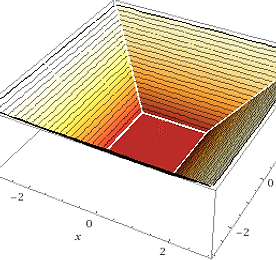 SCPC 2019 본선 5번 풀이. 정육면체 재구성
문제 설명(요약) 3차원 공간에 \(N\)개의 점 \(P_1(x_1,y_1,z_1)\), \(\cdots\), \(P_N(x_N,y_N,z_N)\)이 주어져 있다. (정수좌표) 다음 조건을 만족하는 두 정육면체 \(Q\), \(Q'\)을 생각하자. \(Q\)와 \(Q'\)의 중심은 서로 일치한다. 주어진 \(N\)개의 점은 \(Q\)의 내부 또는 경계에 있으며, 동시에 \(Q'\)의 외부 또는 경계에 있다. 즉, \(Q\)는 바깥쪽 정육면체이고 \(Q'\)은 안쪽 정육면체이다. \(Q\)와 \(Q'\)의 한 변 길이의 차이의 최솟값을 구하시오. 제약 조건: \(N \le 15,000\), \(-10^9 \le x_i, y_i, z_i \le 10^9\) 실행 조건: 테스트 케이스 50개에 대한 실행시간 ..
더보기
SCPC 2019 본선 5번 풀이. 정육면체 재구성
문제 설명(요약) 3차원 공간에 \(N\)개의 점 \(P_1(x_1,y_1,z_1)\), \(\cdots\), \(P_N(x_N,y_N,z_N)\)이 주어져 있다. (정수좌표) 다음 조건을 만족하는 두 정육면체 \(Q\), \(Q'\)을 생각하자. \(Q\)와 \(Q'\)의 중심은 서로 일치한다. 주어진 \(N\)개의 점은 \(Q\)의 내부 또는 경계에 있으며, 동시에 \(Q'\)의 외부 또는 경계에 있다. 즉, \(Q\)는 바깥쪽 정육면체이고 \(Q'\)은 안쪽 정육면체이다. \(Q\)와 \(Q'\)의 한 변 길이의 차이의 최솟값을 구하시오. 제약 조건: \(N \le 15,000\), \(-10^9 \le x_i, y_i, z_i \le 10^9\) 실행 조건: 테스트 케이스 50개에 대한 실행시간 ..
더보기